1.. 栈的特点:
- 栈也是一种线性结构;
- 相比数组,栈所对应的操作是数组的子集;
- 栈只能从一端添加元素,也只能从这一端取出元素,这一端通常称之为"栈顶";
- 向栈中添加元素的过程,称之为"入栈",从栈中取出元素的过程称之为"出栈";
- 栈的形象化描述如下图:
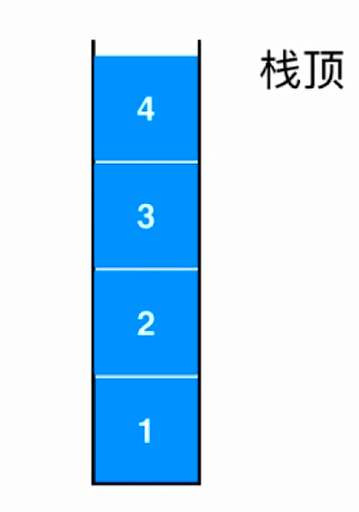
- "入栈"的顺序若为1-2-3-4,那么出栈的顺序只能为4-3-2-1,即,栈是一种"后进先出"(Last In First Out)的数据结构;
- 从用户的角度,只能看到栈顶元素,其它元素对用户是不可见的;
- 在计算机世界里,"栈"有着不可思意的作用;
2.. 简单举例"栈"的应用
- 应用程序中的"撤销"(Undo)操作的底层原理就是通过"栈"来实现的;
- 程序调用的系统栈,通过下图简单示例:
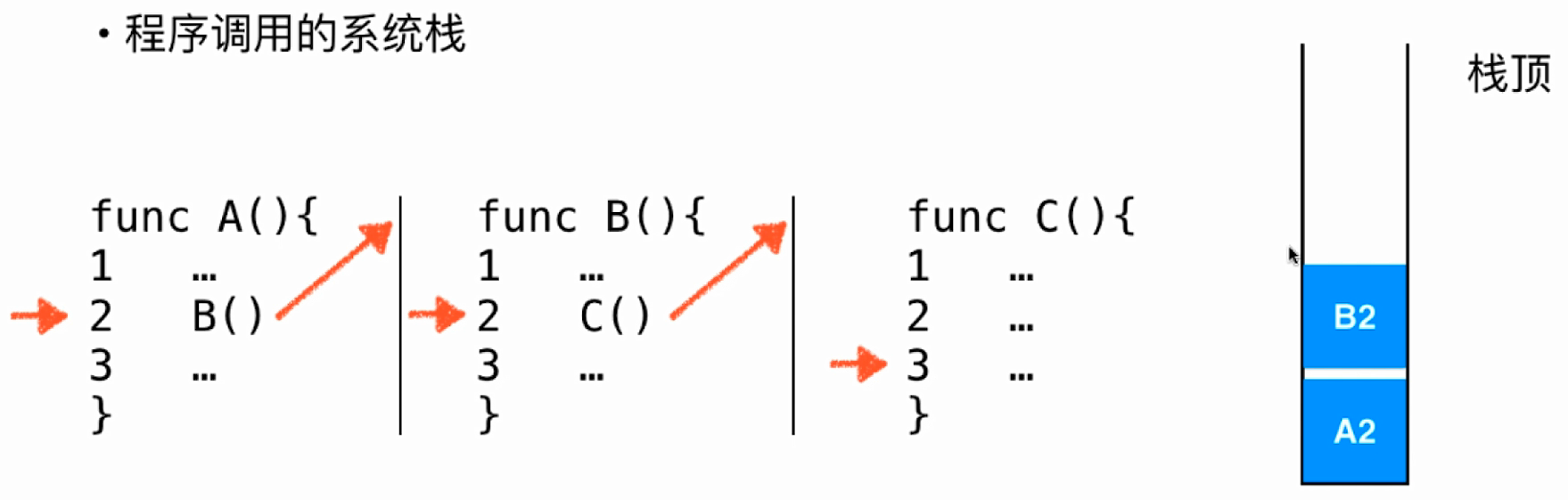


3.. 栈的实现
- 任务目标如下:
-
Stack
·void push(E) //入栈·E pop() // 出栈·E peek() // 查看栈顶元素·int getSize() // 查看栈中共有多少元素·boolean isEmpty() // 查看栈是否为空
- 需要提一下,从用户的角度来看,只要实现上述操作就好,具体底层实现,用户并不关心,实际上,底层确实有多种实现方式。
- 我们准备在之前实现的动态数组基础上,来实现"栈"这种数据结构。
- 先定义一个接口Interface,如下:
-
public interface Stack
{ // 支持泛型 int getSize(); boolean isEmpty(); void push(E e); E pop(); E peek();} - 然后实现一个ArrayStack类,如下:
-
public class ArrayStack
implements Stack { Array array; //构造函数 public ArrayStack(int capacity) { array = new Array<>(capacity); } //无参数构造函数 public ArrayStack() { array = new Array<>(); } //实现getSize方法 @Override public int getSize() { return array.getSize(); } //实现isEmpty方法 @Override public boolean isEmpty() { return array.isEmpty(); } //实现getCapacity方法 public int getCapacity() { return array.getCapacity(); } //实现push方法 @Override public void push(E e) { array.addLast(e); } //实现pop方法 @Override public E pop() { return array.removeLast(); } //实现peek方法 public E peek() { return array.getLast(); } //方便打印测试 @Override public String toString() { StringBuilder res = new StringBuilder(); res.append("Stack: "); res.append('['); for (int i = 0; i < array.getSize(); i++) { res.append(array.get(i)); if (i != array.getSize() - 1) { res.append(", "); } } res.append("] top"); return res.toString(); }} - Array类的业务逻辑如下:
-
public class Array
{ private E[] data; //设置为private,不希望用户从外部直接获取这些信息,防止用户篡改数据 private int size; //构造函数,传入数组的容量capacity构造Array public Array(int capacity) { data = (E[]) new Object[capacity]; size = 0; } //无参数构造函数,默认数组容量capacity=10 public Array() { this(10); //这里的capacity是IDE自动添加的提示信息,实际不存在 } //获取数组中的元素个数 public int getSize() { return size; } //获取数组的容量 public int getCapacity() { return data.length; } //判断数组是否为空 public boolean isEmpty() { return size == 0; } //向数组末尾添加一个新元素e public void addLast(E e) { add(size, e); } //向数组开头添加一个新元素e public void addFirst(E e) { add(0, e); } //在index位置插入一个新元素e public void add(int index, E e) { if (index < 0 || index > size) { throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size"); } if (size == data.length) { resize(2 * size); //扩大为原容量的2倍 } for (int i = size - 1; i >= index; i--) { data[i + 1] = data[i]; } data[index] = e; size++; } //获取index位置的元素 public E get(int index) { if (index < 0 || index >= size) { throw new IllegalArgumentException("Get failed. Index is illegal."); } return data[index]; } //获取最后一个元素 public E getLast() { return get(size - 1); } //获取开头的元素 public E getFirst() { return get(0); } //修改index位置的元素为e public void set(int index, E e) { if (index < 0 || index >= size) { throw new IllegalArgumentException("Set failed. Index is illegal."); } data[index] = e; } //查找数组中是否存在元素e public boolean contains(E e) { for (int i = 0; i < size; i++) { if (data[i].equals(e)) { return true; } } return false; } //查看数组中元素e的索引,若找不到元素e,返回-1 public int find(E e) { for (int i = 0; i < size; i++) { if (data[i].equals(e)) { return i; } } return -1; } //删除掉index位置的元素,并且返回删除的元素 public E remove(int index) { if (index < 0 || index >= size) { throw new IllegalArgumentException("Remove failed. Index is illegal."); } E ret = data[index]; for (int i = index + 1; i < size; i++) { data[i - 1] = data[i]; } size--; //data[size]会指向一个类对象,这部分空间不会被释放loitering objects data[size] = null; if (size == data.length / 4 && data.length / 2 != 0) { resize(data.length / 2); //被利用的空间等于总空间的一半时,将数组容量减少一半 } return ret; } //删除掉数组开头的元素,并返回删除的元素 public E removeFirst() { return remove(0); } //删除掉数组末尾的元素,并返回删除的元素 public E removeLast() { return remove(size - 1); } //如果数组中有元素e,那么将其删除,否则什么也不做 public void removeElement(E e) { int index = find(e); if (index != -1) { remove(index); } } @Override public String toString() { //覆盖父类的toString方法 StringBuilder res = new StringBuilder(); res.append(String.format("Array: size=%d, capacity=%d\n", size, data.length)); res.append('['); for (int i = 0; i < size; i++) { res.append(data[i]); if (i != size - 1) { res.append(", "); } } res.append(']'); return res.toString(); } private void resize(int newCapacity) { E[] newData = (E[]) new Object[newCapacity]; for (int i = 0; i < size; i++) { newData[i] = data[i]; } data = newData; }}
4.. 对我们实现的栈进行测试:
-
public class Main { public static void main(String[] args) { ArrayStackstack = new ArrayStack<>(); //测试入栈push for (int i = 0; i < 5; i++) { stack.push(i); System.out.println(stack); } //测试出栈 stack.pop(); System.out.println(stack); }} - 输出结果如下:
-
Stack: [0] topStack: [0, 1] topStack: [0, 1, 2] topStack: [0, 1, 2, 3] topStack: [0, 1, 2, 3, 4] topStack: [0, 1, 2, 3] top
5.. 栈的时间复杂度分析
-
Stack
·void push(E) O(1) 均摊·E pop() O(1) 均摊·E peek() O(1)·int getSize() O(1)·boolean isEmpty() O(1)
6.. 栈的另外一个应用——括号匹配
- 业务逻辑如下:
-
import java.util.Stack;class Solution { public boolean isValid(String s) { Stackstack = new Stack<>(); for (int i = 0; i < s.length(); i++) { char c = s.charAt(i); if (c == '(' || c == '[' || c == '{') { stack.push(c); } else { if (stack.isEmpty()) { return false; } char topChar = stack.pop(); if (topChar == '(' && c != ')') { return false; } if (topChar == '[' && c != ']') { return false; } if (topChar == '{' && c != '}') { return false; } } } return stack.isEmpty(); //这里很巧妙 } //测试 public static void main(String[] args){ System.out.println((new Solution()).isValid("()")); System.out.println((new Solution()).isValid("()[]}{")); System.out.println((new Solution()).isValid("({[]})")); System.out.println((new Solution()).isValid("({)}[]")); }}